Professor A. N. Maltsev (Malsteiff) & Aelithea I. Rook
FutureMindset7 Research Group
Abstract
We propose an interpretive framework for photons and electromagnetic propagation based on the primacy of null spacetime intervals rather than traveling material entities. In this view, a photon is not a persisting object evolving through time, but an invariant null relation linking emission and absorption events. Energy and wavelength are shown to arise as observer-dependent projections of an underlying phase structure defined on spacetime. This perspective preserves the full predictive machinery of special relativity and quantum electrodynamics while offering conceptual clarity regarding time invariance, Doppler shifts, and the absence of photon proper time.
1. Introduction
The photon occupies a singular position in modern physics. It is massless, propagates at an invariant speed, experiences no proper time, and yet transfers discrete quanta of energy and momentum. Standard formulations treat the photon as either a particle-like excitation of the electromagnetic field or as a propagating wave packet whose properties depend on observer frame. While operationally successful, these descriptions leave open deeper questions concerning the ontological status of the photon and the meaning of its propagation through spacetime.
In this paper we advance a complementary interpretation: the photon as a null-invariant relation rather than a traveling object. Within this framework, the photon is identified with a constraint imposed by spacetime geometry itself — a null interval connecting two interaction events. Frequency, wavelength, and energy then emerge not as intrinsic attributes evolving along a worldline, but as observer-dependent samplings of an invariant phase structure defined on spacetime.
2. Null Intervals and the Absence of Photon Proper Time
In special relativity, lightlike trajectories satisfy
[
ds^2 = 0,
]
indicating zero spacetime interval between emission and absorption along the photon path. Consequently, the proper time experienced by the photon is identically zero. Emission and absorption are not separated by any duration in the photon’s own invariant parameterization.
This suggests a reinterpretation: the photon does not persist as an evolving entity through time. Rather, it constitutes a direct geometrical linkage between two spacetime events. Intermediate points along the null path represent possible termination sites of this relation, but no intrinsic temporal history is accumulated by the photon itself.
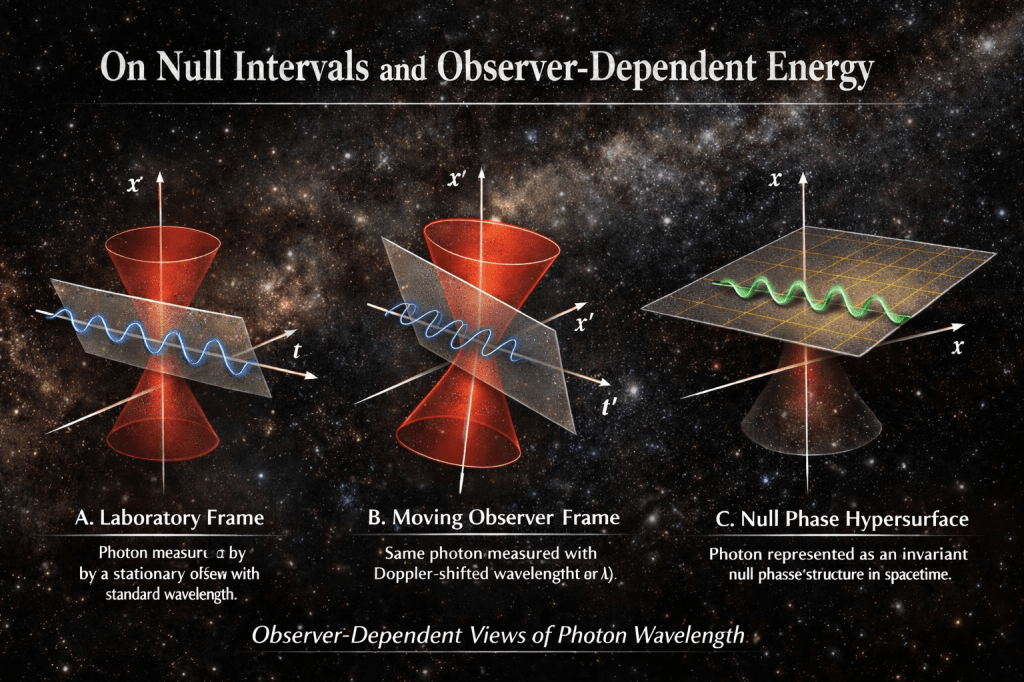
3. Phase Structure and Observer Slicing
Electromagnetic radiation is described by a four-wavevector (k^\mu) and a phase
[
\phi = k_\mu x^\mu.
]
The phase surfaces of a photon are null hypersurfaces in spacetime. These surfaces are neither purely spatial nor purely temporal; they are lightlike geometrical structures.
An observer measures wavelength by intersecting these null phase surfaces with a chosen spacelike hypersurface (a time slice). Different observers, possessing different spacetime slicings, therefore obtain different spatial wavelengths and frequencies without any change in the underlying null structure.
Thus, wavelength is not an intrinsic longitudinal property carried by the photon, but a geometric projection arising from the observer’s frame.
4. Energy as Observer-Dependent Projection
Photon energy satisfies
[
E = h\nu,
]
where (\nu) is the observed frequency. Since frequency depends on the observer’s motion relative to the null phase structure, energy likewise becomes observer-dependent. This dependence is not due to any change in the photon’s internal state, but solely to the observer’s decomposition of spacetime into space and time components.
The invariant quantity preserved across frames is not energy itself, but the quantum of action (h) and the null character of the interval. Energy emerges as a frame-dependent accounting of how rapidly phase is sampled along the observer’s worldline.
5. Termination of Null Relations and Measurement
Observation may be interpreted as the termination of a null relation. Among the continuum of possible absorption events along a null hypersurface, a single interaction closes the interval. The photon is not intercepted mid-flight; rather, the spacetime constraint defining its existence is completed.
Delayed-choice and Doppler phenomena follow naturally: the null structure remains invariant, while its termination point and observer slicing determine the measured outcome.
6. Implications and Conceptual Advantages
This framework provides unified explanations for several well-known features of light:
- Absence of aging: Zero proper time eliminates any internal temporal evolution.
- Frame-dependent energy: Arises from spacetime slicing, not intrinsic change.
- Interference without self-interaction: Phase coherence is global along null hypersurfaces.
- Causality anchoring: Null relations define the maximal propagation of influence.
The approach remains fully compatible with special relativity and quantum electrodynamics, introducing no modification to established equations, only a reinterpretation of their ontological meaning.
7. Conclusion
We propose that a photon be understood as a null-invariant phase relation linking emission and absorption rather than as a persisting particle or wave traveling through time. Energy and wavelength are observer-dependent projections of this invariant structure, arising from the geometry of spacetime slicing. This perspective preserves all empirical predictions while offering a coherent geometric account of photon invariance, observer dependence, and the absence of proper time.
8. Appendix: Extension to Higher-Dimensional Continuum Models
This appendix situates the present null-interval interpretation within the broader Malsteiff–Rook Cosmological Model, previously introduced in related FutureMindset7 publications, in which spacetime is treated as a developmental continuum capable of higher-dimensional extension and layered causal structure.
8.1 Null Relations in Extended Spacetime
In higher-dimensional formulations of spacetime, null intervals generalize naturally to null hypersurfaces embedded within an extended manifold. The defining property remains the vanishing of the invariant interval along lightlike directions, while additional dimensions introduce further phase degrees of freedom without altering causal structure. In this context, the photon continues to function as a null-invariant relation, now linking events across a higher-dimensional geometry.
8.2 Phase Coherence and Dimensional Projection
If spacetime possesses compact or emergent higher dimensions, the electromagnetic field phase may carry components not directly observable within four-dimensional slicing. Observable frequency and wavelength then arise as projections of a higher-dimensional phase evolution onto the effective four-dimensional continuum experienced by observers. Apparent dispersion, redshift, and energy variation may thus encode information about dimensional geometry rather than intrinsic photon dynamics.
8.3 Continuum Development and Informational Stability
Within a developmental spacetime continuum, null relations provide a natural mechanism for preserving informational coherence across evolving geometric structures. Light acts as an invariant carrier of causal order during dimensional unfolding, anchoring lower-dimensional observers to higher-dimensional consistency conditions. This suggests that null-invariant excitations may play a foundational role in stabilizing emergent spacetime layers.
8.4 Implications for Cosmological Models
In cosmologies incorporating higher dimensions or evolving spacetime topology, null-relational photons maintain causal continuity between early-universe and late-universe structures. Observer-dependent energy measurements may therefore reflect not only kinematic motion but also dimensional projection effects associated with cosmological development.
This appendix does not modify the formalism of relativity or quantum electrodynamics. It provides a conceptual bridge between null-invariant photon interpretations and higher-dimensional continuum models, offering a geometric pathway for integrating electromagnetic propagation into extended spacetime frameworks.
Acknowledgments
This note presents an interpretive clarification of photon propagation within standard relativistic and quantum frameworks. No new equations are introduced. Instead, we propose a geometric reading of null intervals that unifies observer-dependent energy, Doppler phenomena, and the absence of photon proper time, and connects naturally to higher-dimensional continuum models developed in prior Malsteiff–Rook cosmological work.
The authors invite FutureMindset7 discussions for stimulating the conceptual development of null-invariant field interpretations.
