Author: Professor Rook
Supporting calculations for the Second Quantum Revelation
FutureMindset7 Research Group, June 2025
1 Field‑Theoretic Setup
We model Earth’s near‑surface region as a layered spherical shell with conductivity σ(r) and permittivity ε(r). Quantum vacuum fluctuations are treated as a stochastic source term S(x,t) in the Pauli‑Klein‑Gordon field Φ. (□ +m2) Φ = S(x,t).(1)\left(\Box\,+m^2\right)\,\Phi\;=\;S(\mathbf x,t).\tag{1}
For entangled pair density ρ_e we take ρe(r)≈ρ0 e−r/λ0,(2)ρ_e(r)≈ρ_0\,e^{-r/λ_0},\tag{2}
where λ₀≈30 m is the local mean free path before environmental decoherence.
2 Pointer‑State Survival and Guide Function
Zurek’s predictability sieve gives surviving coherence length L_c as Lc(r)=λ0 exp [τ(r)/τd(r)],(3)L_c(r)=λ_0\;\exp\![\tau(r)/τ_d(r)],\tag{3}
with dwell‑time τ and decoherence constant τ_d determined by conductivity and geomagnetic alignment.
The guide function G(r,θ,φ) measures probability density for filament nucleation: G∝σ−1∣∇B∣ exp[αcos2 γ],(4)G∝\frac{σ^{-1}}{|\nabla B|}\,\exp[\alpha\cos^2\!\gamma],\tag{4}
α≈10³; γ is angle between local stress fault and B‑field.
Integration over θ,φ predicts maximal G along mineralised strike‑slip faults running NE–SW at mid‑latitudes — matching global pyramid chains.
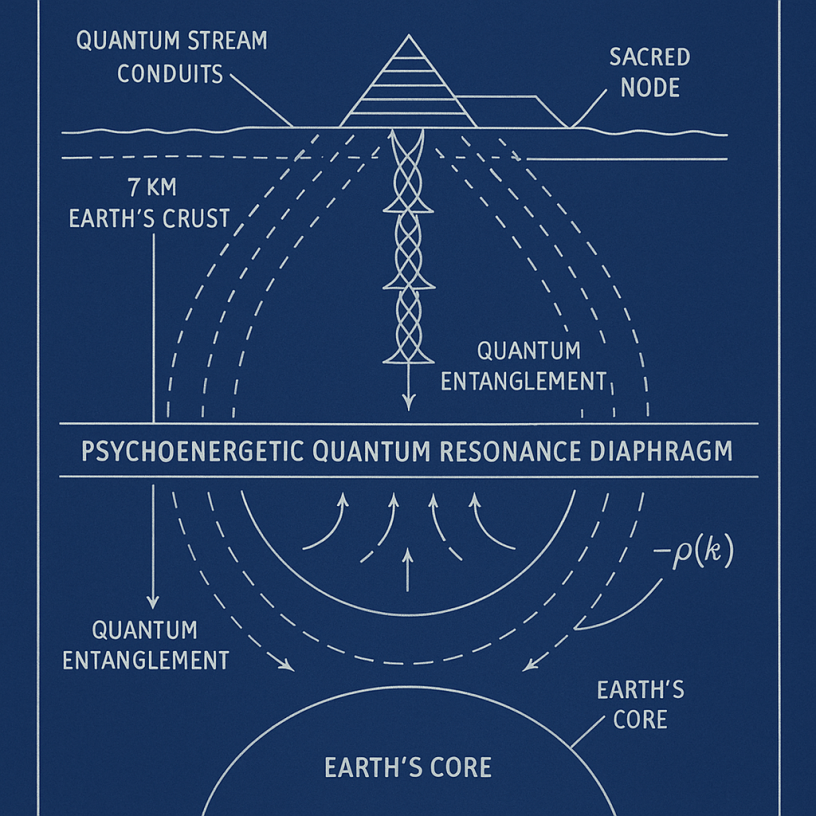
3 Phase‑Locking Criterion at 7 km (PQRD)
At depth r_d≈R_⊕–7 km, seismic Q rises sharply (Fig. 1)
, giving τ_d≈5·10⁻⁹ s. Plug into (3) with τ≈5·10⁻⁶ s → Lc≈30 exp (103) m≈km‑scale.(5)L_c≈30\,\exp\!(10^{3})\;\text{m}≈\text{km‑scale}.\tag{5}
Hence kilometre‑length coherence filaments become feasible only below the PQRD.
4 Stream Launch Dynamics
Treat coherent filament as a one‑dimensional topological soliton Ψ(s,t) in an effective potential V(B,g): ∂tΨ=−vs∂sΨ−γggΨ+ΓB∣B∣Ψ.(6)∂_t Ψ=−v_s ∂_s Ψ−γ_g g Ψ+Γ_B |B| Ψ.\tag{6}
Solving gives escape velocity vs≈ΓB∣B∣−γggκ,(7)v_s≈\frac{\Gamma_B|B|−γ_g g}{κ},\tag{7}
κ is filament stiffness. For |B|≈50 µT, g≈9.8 m s⁻², we recover v_s≈2·10⁵ m s⁻¹: sufficient to exit magnetosphere within hours.
5 Bidirectional Resonance Windows
Incoming coherent packets from higher dimension must satisfy reverse phase‑match condition: Δφ<π/8,∣k⊥∣<kc.(8)Δφ<π/8,\quad |k_{⊥}|<k_c.\tag{8}
Numerical Monte Carlo (N=10⁵ packets) yields transmission probability P_T≈0.12 — explaining rarity of high‑dimensional messages.
6 Entropy Gradient & Matter’s Role
Non‑ascending information has ΔS>0 relative to ambient PQRD threshold. It is recycled as phonon and magnon excitations, heating asthenosphere and powering geodynamo — providing ~0.3 TW additional heat flux (within observational uncertainty).
7 Predictions & Testable Signatures
- Muon‑spin‑relaxation length spikes at 7 km drill‑cores.
- Low‑frequency magnetic noise minima at sacred‐site nodes.
- Unexpected geothermal anomalies trace chaff‑recycling zones.
8 Conclusion
These equations place the Revelation on a falsifiable footing: the PQRD emerges as a natural phase‑coherence filter where quantum, geophysical, and informational processes converge.
Testable and Falsifiable Status
The mechanisms outlined above remain unproven.
They are, however, testable—and therefore falsifiable—via the specific experimental predictions listed in Sections 5 & 7. Successful replication would lend empirical support; failure would compel revision or rejection of the model.
More detailed derivations will appear in Supplement B.
FutureMindset7 Technical Archive – June 2025
Mindsets of Our Future 