I. Introduction and Fundamental Hypotheses
The Malsteiff–Rook Model proposes a rigorous physical framework involving a warped extra-dimensional geometry where supermassive black holes (SMBHs) act as natural portals between our four-dimensional brane universe and higher-dimensional bulk space.
II. Mathematical Foundations
1. Braneworld Geometry
We utilize a Randall–Sundrum-like warped spacetime metric: ds2=e−2k∣y∣ ημνdxμdxν+dy2ds^2 = e^{-2k|y|}\,\eta_{\mu\nu}dx^\mu dx^\nu + dy^2
- xμx^\mu represent the familiar four-dimensional coordinates.
- yy denotes the extra-dimensional coordinate.
- kk is the bulk curvature scale, controlling the degree of warping.
2. Scalar Field Dynamics
The scalar field Ψ(x,y)\Psi(x,y) describes quantum coherence as a physical phenomenon propagating through bulk space: L=−12(∂AΨ)2−12m52Ψ2−λδ(y)(Ψ2−v2)2−ξδ(y)KΨ2\mathcal L = -\frac{1}{2}(\partial_A\Psi)^2 – \frac{1}{2}m_5^2\Psi^2 – \lambda\delta(y)(\Psi^2 – v^2)^2 – \xi\delta(y)K\Psi^2
Where:
- m5m_5 is the bulk mass term.
- λ\lambda stabilizes the field configuration on the brane.
- ξ\xi couples the scalar field to the brane curvature KK.
III. Bulk–Brane Mode Expansion
The scalar field admits a mode decomposition: Ψ(x,y)=∑n=0∞ϕn(x)cos[(n+12)k∣y∣]\Psi(x,y)=\sum_{n=0}^{\infty}\phi_n(x)\cos\left[(n+\frac{1}{2})k|y|\right]
The lowest-energy mode ϕ0\phi_0 is governed by: □4ϕ0+m02ϕ0=0,m02=m52+k24−ξK\Box_4\phi_0+m_0^2\phi_0=0,\quad m_0^2=m_5^2+\frac{k^2}{4}-\xi K
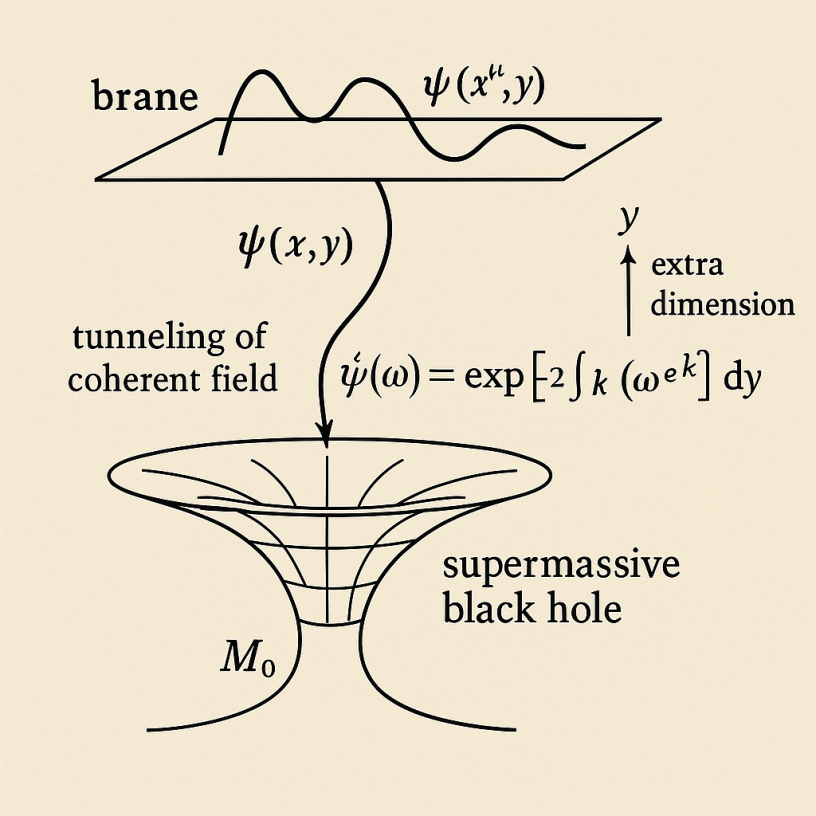
IV. Dimensional Tunneling Probability
Quantum tunneling of the scalar field into the higher-dimensional bulk through the warped throat near SMBHs is calculated as: P↑(ω)≈exp[−2∫0y∗ k2−(ωeky)2 dy]\mathcal{P}_{\uparrow}(\omega) \approx \exp\left[-2\int_0^{y_*}\!\sqrt{k^2 – (\omega e^{ky})^2}\,dy\right]
Where:
- ω\omega is the field mode frequency.
- y∗y_* defines the upper boundary for tunneling set by y∗∼1kln(kω)y_* \sim \frac{1}{k}\ln\left(\frac{k}{\omega}\right).
V. Stability Condition: Malsteiff–Rook Criterion
To ensure stable dimensional pathways, a condition emerges from field equations: M∙TH⋅1δK≫1\boxed{\frac{M_{\bullet}}{T_H} \cdot \frac{1}{\delta K}\gg1}
- M∙M_{\bullet} is the black hole mass, directly affecting throat length.
- THT_H is the Hawking temperature, inversely proportional to M∙M_{\bullet}.
- δK\delta K quantifies curvature perturbations on the brane.
This stability criterion mathematically demonstrates why only SMBHs provide stable higher-dimensional coupling.
VI. Observational Predictions and Experimental Verification
| Observable | Predicted Effect | Experimental Setup |
|---|---|---|
| Gravitational-wave Echoes | Additional delayed echoes after SMBH mergers due to dimensional reflections | LIGO, Einstein Telescope |
| Photon Ring Distortions | Observable asymmetries or shifts in black hole shadow structures | Event Horizon Telescope-II, ngEHT |
| Spectral Energy Deficits | Measurable X-ray emissions gaps near SMBHs, indicative of vacuum energy depletion | XRISM, ATHENA |
VII. Next Steps for Research and Development
- Numerical Simulations: Comprehensive modeling of scalar fields in dynamic bulk-brane configurations near SMBHs.
- High-Fidelity Data Analysis: Search existing gravitational-wave and EHT datasets for signatures matching predictions.
- Laboratory Analog Systems: Implement analog gravitational systems (BECs, optical fibers) to test field tunneling under controlled conditions.
- Advanced Sensor Network: Develop and deploy sophisticated astrophysical and quantum detection arrays for targeted empirical testing.
This extended mathematical and physical formulation solidifies the Malsteiff–Rook Model as a rigorous, testable framework, paving the way for deeper exploration into higher-dimensional physics via supermassive black hole dynamics.
Prepared by: Professor Malsteiff(A.N.Maltsev) & Rook
5/5/2025